Американский математик Вирджиния Василевска-Уильямс (Virginia Vassilevska Williams) нашла максимально быстрый способ умножения квадратных матриц, основанный на известном алгоритме Копперсмита — Винограда.

В информатике матричное умножение становится базовой операцией, часто встречающейся при решении даже тех вычислительных задач, которые, кажется, никакого отношения к матрицам не имеют. Для оценки его сложности вводят матричную экспоненту ω — такое минимальное число, что для любого ε > 0 и любого достаточно большого n количество арифметических операций, необходимых для вычисления произведения двух матриц размером n×n, не превосходит n^{ω + ε}.

Несложно показать, что классический алгоритм перемножения матриц (нахождение суммы произведений элементов из определённой строки матрицы А на соответствующие им элементы из столбца матрицы В) требует n³ умножений и n²•(n – 1) сложений. Долгое время его считали быстрейшим, но в 1969 году германскому математику Фолькеру Штрассену удалось разработать новую методику с ω < 2,808. Штрассен представил алгоритм, имеющий не восемь, а семь умножений чисел, в матричной алгебре М_2×2, но его можно распространить на матрицы более высоких порядков рекурсивно (посредством блочного разбиения матриц), причём на каждом этапе рекурсии будут выполняться всё те же семь умножений.

Недостатками такой методики называют бóльшую (по сравнению с классическим алгоритмом) сложность программирования и большой объём используемой памяти.

Публикация вычислений Штрассена инициировала активные поиски быстрых алгоритмов, и уже через несколько лет учёные заметно снизили оценку величины ω. График изменения ω приведён на рисунке ниже.

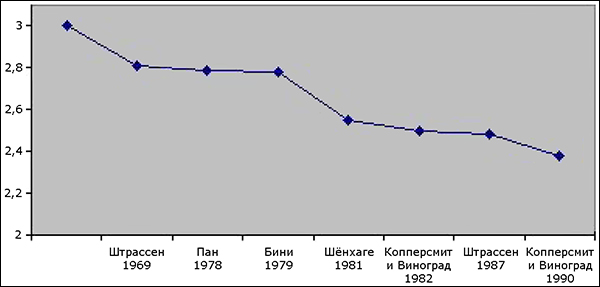Рис. 1. Оценки ω, которые давали разные авторы (иллюстрация из кандидатской диссертации Вирджинии Уильямс).

В 1990 году американцы Дон Копперсмит и Шмуэль Виноград, развившие идеи Штрассена, добились ω < 2,376, после чего уменьшение оценки матричной экспоненты прекратилось. На протяжении двадцати лет алгоритм Копперсмита — Винограда оставался самым быстрым, но в реальных вычислительных задачах не использовался, так как он эффективен только на чрезвычайно больших матрицах.

Поскольку методу Копперсмита — Винограда свойственна рекурсивность (алгоритм выполняется двукратно), сами его авторы предлагали коллегам рассмотреть случаи с большей «глубиной» рекурсии и выяснить, не позволит ли это снизить ω.

Трёхкратное применение алгоритма не давало нужного эффекта, а задача по оценке ω на глубоких уровнях рекурсии оказалась довольно сложной, и некоторые математики поспешили признать значение 2,376 окончательным.

Г-жа Уильямс, однако, продолжила рассмотрение метода Копперсмита — Винограда и нашла несколько упрощённый способ расчёта ω. Испытывая его, она обнаружила, что восьмикратное применение алгоритма позволяет получить новое ограничение: ω < 2,3727.

Остаётся добавить, что истинным значением матричной экспоненты многие специалисты — скажем, те же Копперсмит и Виноград — считают двойку. Доказать это пока никому не удалось.